May 22, 2025 | 15:41
Science
Research
Interpretations of quantum mechanics
Continuing our exploration of the realm of quantum physics, we now turn to the various interpretations of quantum mechanics. These interpretations serve as explanatory frameworks that reconcile the mathematical formalism of quantum mechanics with physical reality. They differ fundamentally on key issues, such as whether quantum mechanics is deterministic or stochastic, local or non-local, which elements of the theory can be considered physically real, and the precise nature of the measurement process, among others.

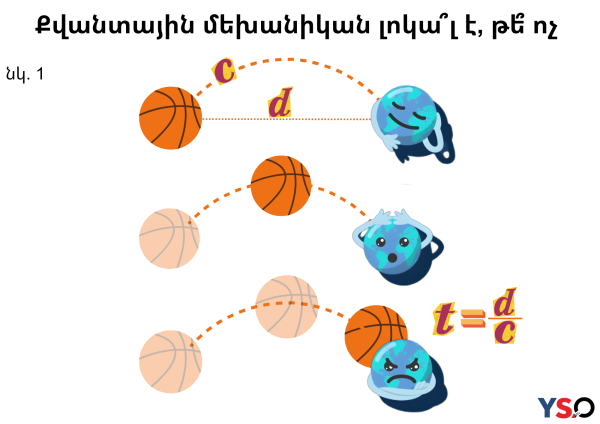
Ըստ դետերմինիստական մոտեցման՝ բնության մեջ ընթացող բոլոր երևույթները կապված են միմյանց հետ պատճառահետևանքային կապերով։ Ստոխաստիկ կամ պատահական մոտեցումը պնդում է հակառակը` ցանկացած երևույթ անկախ է մյուսից, և ցանկացած երևույթ ունի իր իրականացման հավանականությունը։ Տեղային կամ լոկալ նշանակում է, որ օբյեկտի վրա ուղղակի ազդեցություն են թողնում միայն շրջապատի օբյեկտներն ու տեղի ունեցով երևույթները․ մի օբյեկտ մյուսի վրա չի կարող ունենալ զգալի ազդեցություն t=d/c-ից ավելի քիչ ժամանակում, որտեղ d-ն այդ օբյեկների հեռավորությունն է, իսկ c-ն` լույսի արագությունը (տե՛ս նկ. 1)։
Քվանտային ֆիզիկայի տերմինները նույնպես սկզբնական շրջանում տարբեր գիտնականներ տարբեր կերպ են սահմանել։ Օրինակ` Շրյոդինգերը սահմանում էր էլեկտրոնի ալիքային ֆունկցիան՝ որպես նրա լիցքի խտության բաշխում տարածության մեջ, այսինքն՝ ալիքային ֆունկցիան ցույց է տալիս, թե որքան լիցք կա տարածության յուրաքանչյուր կետում կամ յուրաքանչյուր փոքր ծավալում։ Սակայն Մաքս Բորնը վերասահմանեց ալիքային ֆունկցիայի մոդուլի քառակուսին՝ որպես տարածության մեջ էլեկտրոնի բաշխման հավանականության խտություն (տե՛ս մաս 1)։ Փորձերի արդյունքում հերքվեց Շրյոդինգերի տեսակետը և հաստատվեց Բորնինը։ Ինչպես նշել է գիտնական Դավիթ Մերմինը` ամեն տարի ավելանում են քվանային մեխանիկայի ինտերպրետացիաները, և դրանցից ոչ մեկը երբեք չի հերքվել։ Այս պահին ամենամեծ ընդունումն ունի կոպենհագենյան ինտերպրետացիան։
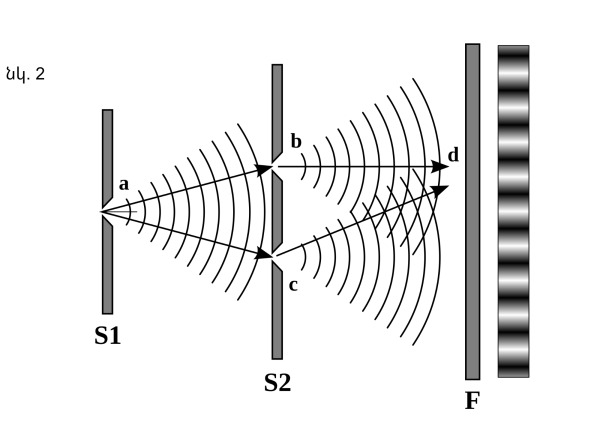
Ֆիզիկայում կրկնակի ճեղքի փորձը (Յունգի փորձը) ցույց է տալիս, որ լույսը և նյութը կարող են դրսևորել ինչպես մասնիկային, այնպես էլ ալիքային վարք: Այս փորձն առաջին անգամ կատարել է Թոմաս Յունգը 1801 թ.՝ ցույց տալով տեսանելի լույսի ալիքային վարքը: Լույսի հետ Յունգի փորձը դասական ֆիզիկայի մաս էր կազմում քվանտային մեխանիկայի և ալիքային-մասնիկային երկակիության մոտեցումների զարգացումից շատ առաջ։ Փորձի ընթացքում ալիքը բաժանվում է երկու առանձին ալիքների (տե՛ս նկ. 2), որոնք հետո վերադրվում են մեկ ալիքի մեջ` ստեղծելով ինտերֆերենցիոն պատկեր:
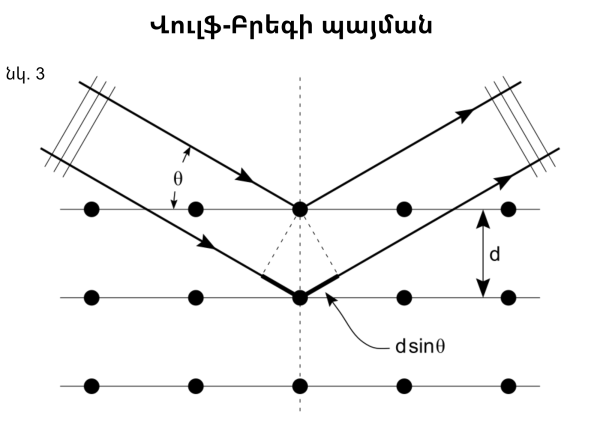
Հետագայում Դը Բրոյլը ցույց տվեց, որ ցանկացած մասնիկ ունի իրեն համապատասխանող ալիքը, որը կոչվում է Դը Բրոյլի ալիք։ 1927 թ. Քլինթոն Դեյվիսոնը և Լեսթեր Ջերմերը, հետազոտելով դանդաղեցված էլեկտրոնների ցրումը նիկելի վրա, հայտնաբերեցին, որ բյուրեղացանցի վրա դիտվում է էլեկտրոնների դիֆրակցիա։ Էլեկտրոնները արագացվել և արձակվել են նիկելի բյուրեղի մակերեսին: Քանի որ բյուրեղը կազմված է կանոնավոր դասավորված ատոմներից, այն գործում է որպես դիֆրակցիոն ցանց էլեկտրոնների համար, եթե դրանք ունեն ալիքային հատկություններ: Դեյվիսոնը և Ջերմերը պտտեցրել են բյուրեղը և դետեկտորը՝ չափելով տարբեր անկյուններով դետեկտորին հասնող էլեկտրոնների քանակը (ինտենսիվությունը): Որոշակի անկյան տակ նրանք դիտել են ինտենսիվության մաքսիմում: Եթե էլեկտրոնները պահեին իրենց որպես մասնիկներ, դրանք պետք է հավասարաչափ ցրվեին։ Այս փորձով հաստատվեց, որ էլեկտրոնները, ինչպես և լույսը, կարող են դրսևորել ալիքային հատկություններ։ Դը Բրոյլի ալիքի երկարությունը տեղադրելով Վուլֆ-Բրեգի պայմանում (որով որոշվում է բյուրեղի վրա ցրված ռենտգենյան ճառագայթման դիֆրակցիոն մաքսիմումների ուղղությունը)՝ էլեկտրոնի համար ստանում ենք նույնպիսի դիֆրակցիոն պատկեր, ինչպիսին կանխագուշակել էր Բրեգը ռենտգենյան ճառագայթների համար (տե՛ս նկ. 3)։ Մինչ Դը Բրոյլի հիպոթեզը ընդունված էր համարել, որ կարող է դիտվել միայն ալիքի դիֆրակցիա։ Ինչպես ֆոտոէֆեկտն է վկայում լույսի մասնիկային բնույթի մասին, այնպես էլ այս փորձը ցույց է տալիս նյութի ալիքային բնույթը և լրացնում է մասնիկ-ալիքային երկակիության տեսությունը։ Էլեկտրոնների դիֆրակցիայի Դեյվիսըն-Ջերմերի փորձից հետո Դը Բրոյլի հիպոթեզը փորձնականորեն հաստատվեց նաև մյուս տարրական մասնիկների համար։ Այս տեսությանն ավելի մանրամասն կծանոթանանք մի փոքր անց։
Ինչպես Շրյոդինգերի կատվի փորձը, Յունգի փորձը հաճախ օգտագործվում է քվանտային մեխանիկայի տարբեր մեկնաբանությունների միջև տարբերություններն ու նմանությունները ցույց տալու համար։ Նիլս Բորը մեկնաբանել է քվանտային փորձերը, այդ թվում նաև Յունգի փորձը` օգտագործելով կոմպլեմենտարության սկզբունքը: Բորի կարծիքով՝ քվանտային համակարգերը դասական չեն, բայց չափումները կարող են տալ միայն դասական արդյունքներ: Դասական հատկություններ միաժամանակ չեն դիտվի քվանտային համակարգում, այսինքն՝ ինտերֆերենցիան կվերանա, եթե ճեղքերում մասնիկներ հայտնաբերվեն:
Կոպենհագենյան ինտերպրետացիա
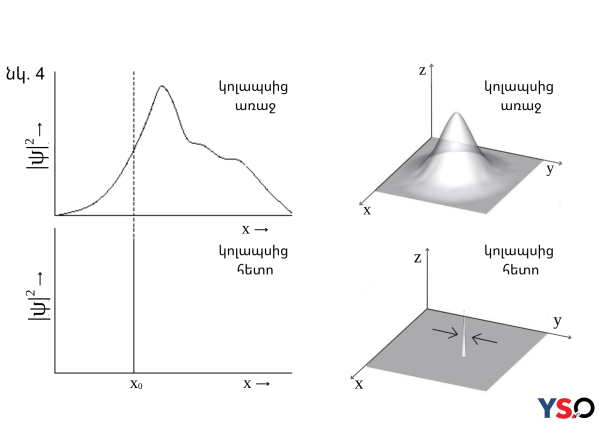
Կոպենհագենյան ինտերպրետացիան ստեղծվել է դեռևս 1927 թ. Կոպենհագենում՝ ֆիզիկոսներ Բորի և Հայզենբերգի կողմից: Այդ օրերից ի վեր՝ բազմաթիվ ֆիզիկոսներ առաջ են քաշել քվանտային մեխանիկայի իրենց ինտերպրետացիաները, սակայն կոպենհագենյան ինտերպրետացիան մինչ օրս համարվում է ամենաընդունելին: Փորձենք հասկանալ ինտերպրետացիայի առանձնահատկությունները: Ըստ կոպենհագենյան ինտերպրետացիայի՝ մասնիկի դիրքը նկարագրվում է ալիքային ֆունկցիայով: Քվանտային մեխանիկայի հիմնական հավասարումը Շրյոդինգերի հավասարումն է: Ըստ այս ինտերպրետացիայի՝ ալիքային ֆունկցիան չունի ֆիզիկական որևէ իմաստ, այն ուղղակի օժանդակ մաթեմատիկական գործիք է, որի մոդուլի քառակուսին տվյալ պահին մասնիկի տվյալ վիճակում գտնվելու հավանականության խտությունն է: Դիտումից հետո տեղի է ունենում ալիքային ֆունկցիայի կոլապս՝ ալիքային ֆունկցիան ակնթարթորեն ընդունում է 0 արժեք բոլոր կետերում, բացի այն կետից, որտեղ հայտնվել է մասնիկը դիտման արդյունքում (տե՛ս նկ. 4): Այսինքն, դիտումից հետո մասնիկը դադարում է սուպերպոզիցիոն վիճակում գտնվելուց՝ հայտնվելով միայն հնարավոր վիճակներից որևէ մեկում: Իրական են համարվում միայն դիտումից հետո ստացված արդյունքները, իսկ մինչև դիտումը մասնիկի վիճակի մասին խոսելն արգելվում է (տե՛ս նկ. 5): Բորը նշում է, որ միակ բանը, որը կարող ենք կանխագուշակել, փորձի արդյունքն է, մնացած հարցերը (օրինակ՝ ինչո՞ւ փորձի արդյունքում մասնիկը հայտվեց հնարավոր վիճակներից հենց այս մեկում) պետք է ուղղել փիլիսոփայությանը կամ ինչպես կասեր Ռիչարդ Ֆեյնմանը՝ լռի՛ր ու հաշվա՛րկդ արա:
Այստեղից երկու շատ կարևոր հետևություններ կարող ենք անել․ առանց դիտողի՝ իրականություն գոյություն չունի, և իրականությունը «ստեղծվում է» դիտման հետևանքով: Շատերը կարող են հարցնել՝ իսկ եթե դիտողը կո՞ւյր է... Դիտող ասելով մենք հասկանում ենք անձ, որ ընդունակ է տեղեկություն ստանալու ոչ թե միայն աչքերով, այլ ընդհանրապես զգայարաններով: Էյնշտեյնը, դժգոհելով այն հանգամանքից, որ քվանտային մեխանիկան կասկածի տակ է դնում օբյեկտիվ իրականությունը, ասել է. «Դուք իրո՞ք կարծում եք, որ դիտողի բացակայությամբ Լուսինը կդադարի գոյություն ունենալուց»: Իրականում սա կապված է մեկ այլ քվանտային երևույթի՝ քվանտային դեկոհերենտության հետ: Քանի որ Լուսինը անդադար փոխազդում է իրեն շրջապատող միջավայրի՝ Երկրի ջերմային ճառագայթման, Արևի լույսի, Արեգակնային քամիների և մի շարք այլ օբյեկտների հետ, արդյունքում այն կորցնում է քվանտային կոհերենտությունը, այլ կերպ ասած՝ քվանտային սուպերպոզիցիայում գտնվելու հատկությունը: Հենց դեկոհերենտության հետևանքով են օբյեկտները կորցնում իրենց քվանտային հատկությունները և մեր կողմից ընկալվում որպես դասական օբյեկտներ: Այդ պատճառով, եթե նույնիսկ բոլոր մարդիկ միաժամանակ դադարեն Լուսնին հետևելուց, շրջապատող միջավայրը կշարունակի «դիտել» նրան, այսինքն՝ այն չի դադարի գոյություն ունենալուց, և նույնիսկ կույր մարդը կարող է թեկուզ մակընթացությունների և տեղատվությունների միջոցով (որոնք, կարելի է ասել, քվանտային խճճվածության մեջ են Լուսնի հետ) իմանալ Լուսնի գոյության մասին:
Դասական աշխարհում, եթե մենք հստակ իմանանք մասնիկի դիրքը, շարժման հետագիծը և սկզբնական պայմանները, այսինքն՝ փորձից առաջ և ընթացքում ունենանք որոշակի տեղեկություն մասնիկի մասին, կարող ենք հստակ որոշել փորձի արդյունքում ստացվող մասնիկի վիճակը: Բայց քվանտային աշխարհում մենք ոչինչ չգիտենք մինչև փորձը: Չկա թաքնված որևէ մեխանիզմ, որ կարող է հստակ կանխագուշակել, թե մասնիկը հնարավոր վիճակներից որում կհայտնվի հաջորդ պահին. մենք գիտենք միայն դրա հավանականության խտությունը: Այդ պատճառով կոպենհագենյան ինտերպրետացիայում, կարելի է ասել, քվանտային մեխանիկան ունի հավանականային բնույթ:
Շատ աշխարհների ինտերպրետացիա
Իսկ ի՞նչ, եթե ալիքային ֆունկցիան երբեք էլ կոլապսի չի ենթարկվել։ Խուսափելու համար ալիքային ֆունկցիայի կոլապսից՝ ամերիկացի ֆիզիկոս Հյու Էվերեթթ III-ը առաջարկեց քվանտային մեխանիկայի շատ աշխարհների ինտերպրետացիան (Many-worlds interpretation - MWI)։
Ենթադրենք՝ մենք ունենք միայն մեկ էլեկտրոն․ ի վերջո ինչպե՞ս կարող է մեկ մասնիկը ինտերֆերենցիայի ենթարկվել ինքն իր հետ։ Եթե դիմենք մասնիկ-ալիքային երկակիության սկզբունքին, կարող ենք էլեկտրոնը պատկերացնել որպես ալիք, որը կանցնի երկու ճեղքերով և ինտերֆերենցիոն պատկեր կառաջացնի։ Իսկ եթե մենք ուզում ենք մեկնաբանել ինտերֆերենցիայի երևույթը՝ էլեկտրոնին վերաբերվելով հենց որպես մասնի՞կ։ Կոպենհագենյան ինտերպրետացիայում էլեկտրոնի բոլոր հետագծերը վերադրվում են այն աշխարհում, որում գտնվում է դիտորդը։ Մեկ այլ մոտեցում պնդում է, որ Յունգի փորձը կարելի է հասկանալ այսպես. կան բազմաթիվ զուգահեռ աշխարհներ, և էլեկտրոնի հետագծերը երբեք չեն վերադրվում, յուրաքանչյուր հետագիծ շարունակում է գոյություն ունենալ մնացածից անկախ՝ առանձին աշխարհում։ Այն մասերում, որտեղ էլեկտրոնն ավելի հաճախ է հայտնվում, առաջանում են ինտերֆերենցիոն պատկերի լուսավոր հատվածները, մյուսներում` մութ հատվածները։
Եկենք նախ հասկանանք, թե ինչո՞ւ առաջարկվեց նոր մեկնաբանություն, և ինչո՞վ կոպենհագենյանը չէր բավարարում ֆիզիկոսներին։ Հյու Էվերեթթը փորձում էր լուծել առաջացած խնդիրներից մեկը, որն ի հայտ էր գալիս կոպենհագենյան մեկնաբանության մեջ` չափման խնդիրը։ Տեսությունը պահանջում էր դիտորդներին վերաբերվել որպես տեսության կողմից նկարագրված համակարգից դուրս, արտաքին մաս: Նա կարծում էր, որ դրա պատճառով է, որ տեսությունը չի կարողանում ապահովել տիեզերքի հաստատուն, շարունակական նկարագրությունը: Էվերեթթն առաջարկեց մի նոր մոտեցում` MWI-ը։ Մեր նախորդ հոդվածում մենք պատկերացնում էինք Շրյոդինգերի կատվին 2 վիճակների սուպերպոզիցիայում, իսկ ինչո՞ւ միայն կատվին, չե՞նք կարող նույն սկզբունքը կիրառել և՛ ատոմի ռադիոակտիվ տրոհման, և՛ մեր, և՛ ընդհանրապես ամբողջ աշխարհի վրա։ Միգուցե երբ մենք բացում ենք արկղը և գտնում կատվին կենդանի վիճակում, դա այն պատճառով է, որ մենք գտնվում ենք բազմաթիվ զուգահեռ աշխարհներից մեկում, որում կատուն կենդանի էր մնացել։ Կա նաև ուրիշ զուգահեռ աշխարհ, որում ռադիոակտիվ տրոհումը տեղի է ունեցել, և մեր մեկ ուրիշ տարբերակ տեսնում է կատվին սատկած վիճակում (տե՛ս նկ. 6)։
Ըստ Էվերեթթի՝ տիեզերքում կան բազմաթիվ աշխարհներ, բացի այն աշխարհից, որը մենք գիտենք: Մասնավորապես, ամեն անգամ, երբ կատարվում է հնարավոր տարբեր արդյունքներով փորձ, ստացվում են բոլոր արդյունքները, յուրաքանչյուրը՝ նորաստեղծ տարբեր աշխարհում, նույնիսկ եթե մենք տեղյակ ենք միայն մեր տեսած արդյունքով աշխարհից: Իսկ ի՞նչ է աշխարհը։ Այն մաթեմատիկական սահմանում չունի և հիմնված է միայն մեր պատկերացումների վրա։ Աշխարհի սահմանումը՝ որպես այն ամենը, ինչ գոյություն ունի, այս դեպքում չի գործում: Ամեն ինչ, որ գոյություն ունի, Տիեզերքն է, և կա միայն մեկ Տիեզերք: Տիեզերքը ներառում է բազմաթիվ աշխարհներ, մեր ներկա աշխարհն ունի յուրահատուկ անցյալ և ապագա:
Համաձայն այս ինտերպրետացիայի՝ աշխարհը, որը որոշվում է ժամանակի ինչ-որ պահի, համապատասխանում է եզակի աշխարհի անցյալում, բայց մի շարք աշխարհների ապագայում: Իսկ ո՞վ եմ ես՝ որպես դիտորդ։ Ես այնպիսի գործիք եմ, ինչպիսին են Երկիրը, կատուն և այլն: «Ես»-ը որոշվում է ժամանակի որոշակի պահի` իմ մարմնի և ուղեղի վիճակի ամբողջական (դասական) նկարագրությամբ: Չնայած, որ իմ անունը Տաթևիկ է, «Ես»-ը և «Տաթևիկ»-ը նույն մարդուն չեն վերաբերում: Ներկա պահին տարբեր աշխարհներում կան շատ տարբեր «Տաթևիկներ» (յուրաքանչյուր աշխարհում մեկից ոչ ավելի), բայց ասել, որ հիմա կա մեկ այլ «ես», անիմաստ է։ Ես ունեմ որոշակիորեն սահմանված անցյալ, բայց ոչ որոշակի ապագա։ Ամեն անգամ, երբ ես կատարում եմ փորձ՝ մի քանի հնարավոր ելքերով, ինձ թվում է միայն, որ ստացվում է մեկ հստակ արդյունք: Իսկապես, այդ կոնկրետ արդյունքը ստացած «Տաթևիկը» այսպես է մտածում։ Փորձից առաջ «Տաթևիկը»-ը համապատասխանում է բազմաթիվ «Տաթևիկ»-ների, որոնք ստանում են հնարավոր բոլոր արդյունքները:
Արդյո՞ք անհրաժեշտ էր ստեղծել նման տեսություն միայն ալիքային ֆունկցիայի կոլապսից խուսափելու համար։ Բայց չէ՞ որ կոպենհագենյան ինտերպրետացիայում նույնպես գոյություն ունի ալտերնատիվ իրականությունների գաղափարը հենց սուպերպոզիցիոն վիճակի մեջ։ Տարբերությունն այն է, որ կոպենհագենյան մեկնաբանության մեջ այդ իրականությունները վերադրվում են ալիքային ֆունկցիայի կոլապսից հետո, իսկ այս դեպքում դրանք շարունակում են գոյություն ունենալ առանձին-առանձին։ Մաթեմատիկական տեսանկյունից սա շատ լավ մեկնաբանություն է, քանի որ քվանտային մեխանիկայում չկար որևէ բան, որ պահանջում էր ալիքային ֆունկցիայի կոլապսը, այն նաև չի ավելացնում բազմաթիվ նոր հասկացություններ քվանտային մեխանիկայում։
Հարաբերական քվանտային մեխանիկա
Հարաբերական քվանտային մեխանիկան (Relational Quantum Mechanics - RQM) ամենաթարմն է քվանտային մեխանիկայի մեկնաբանություններից, որոնք այսօր լայնորեն քննարկվում են: Այն առաջարկվել է 1996 թ. Ռովելիի կողմից` փորձելով հիմք ստեղծել քվանտային գրավիտացիայի տեսության համար։ Տեսության ֆիզիկական բովանդակությունը կապված է ոչ թե առարկաների, այլ նրանց միջև հարաբերությունների հետ։ Հարաբերական քվանտային մեխանիկայի հիմքում ընկած է այն գաղափարը, որ ինչպես հարաբերականության հատուկ տեսության մեջ, տարբեր դիտորդներ կարող են տարբեր ձևով տեսնել միևնույն երևույթը։ Հարաբերական քվանտային մեխանիկան պնդում է, որ «վիճակ» հասկացությունը նկարագրում է ոչ թե դիտարկվող համակարգը, այլ համակարգի և նրա դիտորդի կամ դիտորդների միջև հարաբերությունը կամ հարաբերակցությունը:
Ռովելին ասում է. «Քվանտային մեխանիկան այլ համակարգերի նկատմամբ ֆիզիկական համակարգերի ֆիզիկական նկարագրության տեսություն է, և սա աշխարհի ամբողջական նկարագրությունն է»։
Այս մոտեցումը, ըստ էության, բավականին նման է կոպենհագենյան մեկնաբանությանը, բայց մի կարևոր տարբերությամբ. կոպենհագենյան մեկնաբանության մեջ ենթադրվում է, որ մակրոսկոպիկ աշխարհն իր բնույթով դասական է, և ալիքային ֆունկցիայի կոլապսը տեղի է ունենում, երբ քվանտային համակարգը փոխազդում է մակրոսկոպիկ ապարատի հետ: Այս ինտերպրետացիան պնդում է, որ քվանտային մեխանիկան ալիքային ֆունկցիայի կամ քվանտային վիճակի մասին չէ, այլ ֆիզիկական փոփոխականների արժեքների մասին։ RQM-ը ներառում է միայն ֆիզիկական համակարգեր և փոփոխականներ, որոնք կարող են արժեքներ ընդունել, ինչպես դասական մեխանիկայում: Օրինակ՝ այն փաստը, որ մասնիկը որոշակի t պահի գտնվում է x կոորդինատ ունեցող կետում, կոչվում է «իրադարձություն» կամ «քվանտային իրադարձություն»: Քվանտային տեսությունը նման իրադարձությունների մասին է: Այնուամենայնիվ, քվանտային մեխանիկայի փաստերի և դասական մեխանիկայի փաստերի միջև կա երկու տարբերություն: Դասական մեխանիկայում կան երկու ընդհանուր պայմաններ, որոնք չեն իրագործվում RQM-ում.
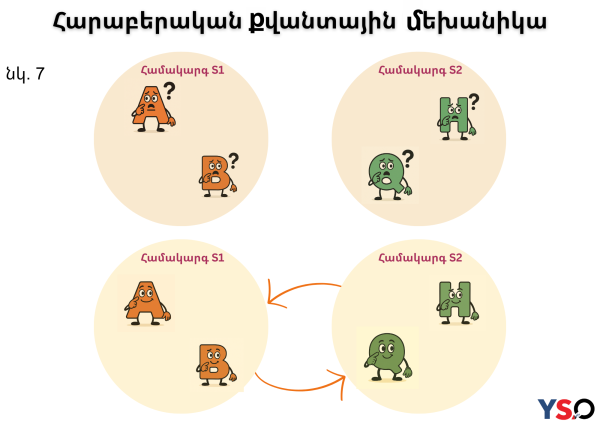
ա) Դասական մեխանիկայում համակարգի բոլոր փոփոխականներն ամեն պահի արժեք ունեն: RQM-ը, ընդհակառակը, ենթադրում է, որ բնության մեջ դա ընդհանրապես այդպես չէ: Ֆիզիկական փոփոխականները արժեքներ ունեն միայն ժամանակի որոշակի պահերի, իսկ մյուս պահերին դրանք արժեքներ չունեն: Կարող ենք ասել, որ իրադարձությունները դիսկրետ են (ոչ անընդհատ)։ Փոփոխականներն ունեն արժեքներ, երբ համակարգը ներգործում է մեկ այլ համակարգի վրա: Որպեսզի S1 համակարգի A փոփոխականը ընդունի արժեք, այդ համակարգը պետք է փոխազդի մեկ այլ S2 համակարգի հետ (տե՛ս նկ. 7)։
բ) Դասական մեխանիկայի երկրորդ պայմանը, որը չի գործում RQM-ում, այն է, որ փոփոխականները վերցնում են բացարձակ արժեքներ՝ անկախ այլ համակարգերից: Փոխարենը RQM-ը ենթադրում է, որ ֆիզիկական բոլոր փոփոխականները հարաբերական են:
Դը Բրոյլ-Բոմի «ուղղորդող-ալիքի» ինտերպրետացիա
Էլեկտրոնը և՛ մասնիկ, և՛ ալի՞ք…
Գիտնական Լուի դը Բրոյլը ունեցել է շատ հետաքրքիր վարկած մասնիկ-ալիքային դուալիզմի մասին: Նա առաջին գիտնականներից էր, որ կարծում էր՝ եթե ինչ-որ բան, որը նախկինում մարդիկ ընդունում էին որպես ալիք, օրինակ՝ լույսը, կարելի է ներկայացնել նաև որպես մասնիկ, ապա ինչ-որ բան, որ մենք նախկինում ընդունում էինք որպես մասնիկ, օրինակ՝ էլեկտրոնը, կարող ենք դիտարկել նաև որպես ալիք: Նա չէր պնդում, որ էլեկտրոնը միաժամանակ և՛ մասնիկ է, և՛ ալիք, այլ ասում էր, որ հնարավոր է գոյություն ունեն 2 առանձին օբյեկտներ՝ ինչ-որ ալիք և ինչ-որ մասնիկ, որոնք միասին առաջացնում են այն երևույթները, որոնք մենք տեսնում ենք փորձերի ժամանակ: Իր վարկածը նա առաջ է բերել նույն գիտաժողովի ժամանակ, երբ Բորը ներկայացնում էր կոպենհագենյան ինտերպրետացիան: Շատ առումներով նրա ենթադրություններն այնքան բնական ու հասկանալի էին, այնքան լավ էին բացատրում մասնիկ-ալիքային երկվությունը, որ տարիներ անց քվանտային մեխանիկայով զբաղվող հանճարներից Ջոն Բելլն ասել է. «Ես չեմ հասկանում՝ ինչու մարդիկ այսքան միաձայն անտեսեցին այս վարկածը»:
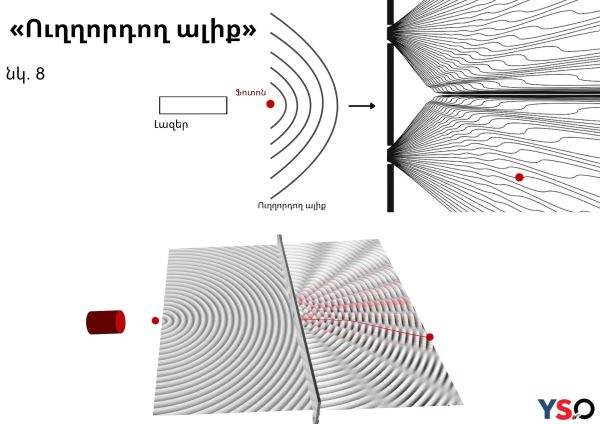
Դը Բրոյլը կարծում էր, որ գոյություն ունի և՛ ալիք, և՛ մասնիկ, և որ ալիքը, որին անվանել են «ուղղորդող-ալիք», տանում է մասնիկի նշանակության վայրը այնպես, ինչպես ծովի ալիքն է «ուղղորդում» նավաբեկությունից մնացած իրերին դեպի ափ: Յունգի փորձում ուղղորդող-ալիքը միաժամանակ անցնում է երկու ճեղքով: Մասնիկներն իրենց շարժումը սկսում են իրարից փոքր-ինչ շեղված կամ մի փոքր տարբեր ուղություններով, և յուրաքանչյուրը, հետևելով իրեն ուղղորդող ալիքին, առաջացնում է մեզ հայտնի ինտերֆերենցիոն պատկերը (տե՛ս նկ. 8): Մենք տեսնում ենք միայն մասնիկներ, իսկ ալիքի գոյության մասին կարող ենք միայն ենթադրել՝ ուսումնասիրելով մասնիկների շարժումները: Բայց մի շարք գիտնականների «շնորհիվ»՝ այս մտքերը հավանության չարժանացան․ Դը Բրոյլը հրաժարվեց իր մտքերը ներկայացնելուց, և դրանք տարիների ընթացքում մոռացվեցին: Տարիներ անց գիտնական Բոմը, չիմանալով Դը Բրոյլի վարկածի մասին, եկել է նույն եզրահանգումներին: Դրա հետևանքով քվանտային մեխանիկայի «ուղղորդող-ալիքի» ինտերպրետացիան հաճախ նաև անվանում են Դը Բրոյլ-Բոմի ինտերպրետացիա:
Մաթեմատիկական տեսանկյունից Բոմն առաջարկեց կոմպլեքս ալիքային ֆունկցիայի համար՝ Շրյոդինգերի մեկ հավասարման փոխարեն դիտարկել երկու իրական հավասարումներ երկու իրական մեծությունների՝ ալիքային ֆունկցիայի R լայնույթի և S փուլի համար:
Դը Բրոյլ-Բոմի ինտերպրետացիան շատ էական տարբերություն ունի կոպենհագենյան ինտերպրետացիայից: Ըստ կոպենհագենյան ինտերպրետացիայի՝ մինչև դիտումը, օրինակ՝ արկղը բացելը, մենք ոչինչ չգիտենք կատվի մասին, և արկղը բացելուց հետո է միայն կատուն ինչ-որ վերջնական վիճակ ստանում՝ ողջ կամ մեռած: Իսկ Դը Բրոյլ-Բոմի ինտերպրետացիայի համաձայն՝ կատուն ողջ է կամ մեռած՝ անկախ մեր դիտելուց․ արկղը բացելուց հետո մենք միայն փաստն ենք արձանագրում:
Հարց է առաջանում, թե ինչու այս ինտերպրետացիան այդպես էլ «դպրոցական դասագրքեր չմտավ»: Չէ՞ որ այն տալիս էր բարդ հարցերին պարզ ու ակնհայտ պատասխաններ: Դա այնքան էլ մեծ գաղտնիք չէ․ բազմաթիվ գիտնականներ, այդ թվում՝ Բորը, գործադրեցին իրենց ողջ ջանքերը այս ինտերպրետացիան նսեմացնելու համար: Չնայած դրան՝ այժմ շատ գիտնականներ այս ինտերպրետացիան համարում են անհերքելի, քանի որ այն հիմնված է Շրյոդինգերի հավասարման վրա, և դրա համար նրա արդյունքները լիովին համապատասխանում են փորձերի արդյունքներին:
Հոդվածը պատրաստեցին ԵՊՀ ֆիզիկայի ինստիտուտին առընթեր գործող օպտիկների միջազգային կազմակերպության ուսանողական մասնաճյուղի («YSO Student Chapter») ներկայացուցիչները

